用js实现二叉树的定义和基本操作
树是计算机科学中经常用到的一种数据结构。树是一种非线性的数据结构,以分层的方式存储数据。树被用来存储具有层级关系的数据,比如文件系统中的文件;树还被用来存储有序列表。
二叉树具有诸多优点。相对于链表来说,二叉树在进行查找时速度非常快,而相对于数组来说,为二叉树添加或删除元素也非常快。
二叉树
二叉树是一种特殊的树,表现在它的子节点个数不超过两个。且二叉树的子树有左右之分,其次序不能任意颠倒。
在实现二叉树时,采用的存储结构为链式存储结构,链式结构的意思是采用一个链表来存储一颗二叉树,二叉树中每一个节点用链表的一个节点来存储,在二叉树中,节点结构至少有三个域:数据域data,左指针域left,右指针域right,如下图所示:
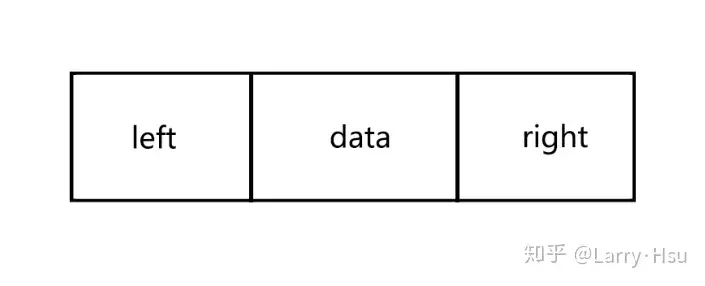
二叉链表的存储结构描述如下:
class Node{
constructor(data, left, right){
this.data = data;
this.left = left;
this.right = right;
this.count = 1;
}
}
与图1不同之处在于多了一个count变量,这个变量的作用在于,在向二叉排序树中插入节点时,如果发现有已经有相同的节点值了,就放弃插入,但是将该节点的count变量加一,这是为了后面实现统计文本中不同的单词数量而设计的。
使用不同的存储结构,实现二叉树的链表的算法也不同。因此接下来的算法全都基于当前所选的存储结构。
其次,将要实现的并不是普通的二叉树,而是二叉排序树,其定义为:
二叉排序树或者是一棵空树,或者是具有下列性质的二叉树:
(1)若左子树不空,则左子树上所有结点的值均小于它的根结点的值;
(2)若右子树不空,则右子树上所有结点的值均大于它的根结点的值;
(3)左、右子树也分别为二叉排序树;
(4)没有键值相等的节点。
二叉排序树
在二叉排序树的实现了一些基本操作:插入节点,删除节点,寻找节点,以及获取最小值和最大值。
代码框架:
class BSTree {
constructor() {
this.root = null;
}
// 删除一个节点
_removeNode(node, data) {
}
// 删除给定的数据节点
remove(data) {
this.root = this._removeNode(this.root, data);
}
// 向二叉树中插入节点
insert(data) {
}
// 寻找给定数据的节点
find(data) {
}
// 获得最小值的节点
getMinNode(node = this.root) {
}
// 获得最大值的节点
getMaxNode(node = this.root) {
}
}
实现二叉排序树的各种方法
首先是insert(data)方法,从总体上来说,插入操作可以分为两步,新建值为data的节点,然后在二叉排序树中找到合适的位置插入即可。
建立以data为值的新的节点比较容易,只要
let newNode = new Node(data, null, null);
即可,关键就在于如何找到正确的插入位置。
这里使用parentNode来记录当前节点的父节点,初始时,该变量为null,当前节点为currNode,初始时为该二叉树的根节点。
- 如果在插入时,root节点为空,则直接将新节点赋给root节点即可。
- 如果新的节点值小于当前节点值,说明待插入的位置应在在当前节点的左子树上,那么在大于时,就应该在当前节点的右子树上。进而更新当前节点所指向的节点,直到当前节点为空时,说明找到了正确的插入位置。
insert()的具体代码如下:
// 向二叉树中插入节点
insert(data) {
let newNode = new Node(data, null, null);
if (this.root == null) {
this.root = newNode;
} else {
let currNode = this.root;
let parentNode = null;
while (true) {
parentNode = currNode;
if (newNode.data < currNode.data) {
currNode = currNode.left; // 更新当前指点的指向
if (!currNode) { // 当前节点为空时,说明找到了正确的插入位置
parentNode.left = newNode;
break;
}
} else if (newNode.data > currNode.data) {
currNode = currNode.right; // 更新当前指点的指向
if (!currNode) { // // 当前节点为空时,说明找到了正确的插入位置
parentNode.right = newNode;
break;
}
} else if (newNode.data == currNode.data) {
// 如果给定的数据再次出现,就更新计数值
currNode.count++;
break;
}
}
}
}
寻找最小值函数getMinNode(),该方法较为简单,因为是一个二叉排序树,所以最小值永远在最左边的分支上,故而一直沿着左分支走到头就是最小值了。
// 获得最小值的节点
getMinNode(node = this.root) {
let currNode = node;
while (currNode.left) {
currNode = currNode.left;
}
return currNode;
}
最大值也是同样的道理:
// 获得最大值的节点
getMaxNode(node = this.root) {
let currNode = node;
while (currNode.right) {
currNode = currNode.right;
}
return currNode;
}
find()方法,在二叉树排序树中寻找给定的数据,比较简单:
// 寻找给定数据的节点
find(data) {
let currNode = this.root;
while (currNode) {
if (currNode.data == data) {
return currNode;
} else if (data < currNode.data) {
currNode = currNode.left;
} else {
currNode = currNode.right;
}
}
return null;
}
接下来时较为复杂一些的remove()方法,由于删除节点操作使用到了递归的操作,所以单独定义了一个函数:
_removeNode(node, data){}
这里在_removeNode()的方法中实现真正的删除操作。该函数的功能是删除以data为值的节点,函数名称前面有个下划线表示不应该在实例中调用此函数。
这里在remove()方法中调用了这个函数:
remove(data){
this.root = this._removeNode(this.root, data);
}
在删除节点时,一共可以分为三种情况:
- 待删除的节点是叶子节点。
- 待删除的节点没有左子节点,或者没有右子节点。
- 待删除的节点的左右子节点均存在。
当待删除的节点时叶子节点时,这种情况比较简单,直接将待删除的节点置空返回即可。
当待删除的节点没有左子节点时,返回该节点的右孩子节点,并删除该节点。待删除节点没有右节点时类似处理。
比较麻烦的是最后一种情况,待删除的节点的左右子节点均存在时,可以有两种做法:要么查找待删除节点左子树上的最大值,要么查找其右子树上的最小值。
这里使用查找其右子树上的最小值的方法。在找到待删除节点的右子树上的最小值后,创建一个临时节点,将临时节点上的值复制到待删除节点,然后再删除临时节点。
// 删除一个节点
_removeNode(node, data) {
if (node == null) {
return null;
}
if (data == node.data) {
// 叶子节点
if (node.left == null && node.right == null) {
return null;
}
// 没有左节点的节点
if (node.left == null) return node.right;
//没有右节点的节点
if (node.right == null) return node.left;
// 有两个节点的节点
/*
做法:
找到待删除节点的右子树上的最小值创建一个临时节点。
将临时节点上的值复制到待删除节点,然后再删除临时节点
*/
// 寻找右子树上的最小值
let tmpNode = this.getMinNode(node.right);
node.data = tmpNode.data;
node.right = this._removeNode(node.right, tmpNode.data);
return node;
} else if (data < node.data) { // 待删除节点在左子树上
node.left = this._removeNode(node.left, data);
return node;
} else { // 待删除节点在右子树上
node.right = this._removeNode(node.right, data);
return node;
}
}
该函数使用了递归的操作来删除一个节点,如果传入待删除的数据值正好等于传入的节点的数据值时,就开始判断是上面提到的3中情况的那一种。如果待删除数据值小于当前节点数据值,则说明待删除的数据在当前节点的左子树上,反之在右子树上。
测试
由于准备将二叉排序树的遍历操作写在下一篇中,所以担心方法可能写错了的小伙伴可能展示无法测试所写的插入和删除操作正确与否。先用写的获取最大值和最小值来测试下吧。
let myTree = new BSTree();
myTree.insert(20);
myTree.insert(13);
myTree.insert(7);
myTree.insert(9);
myTree.insert(15);
myTree.insert(14);
myTree.insert(42);
myTree.insert(22);
myTree.insert(21);
myTree.insert(24);
myTree.insert(57);
新建后的二叉排序树如下图所示:
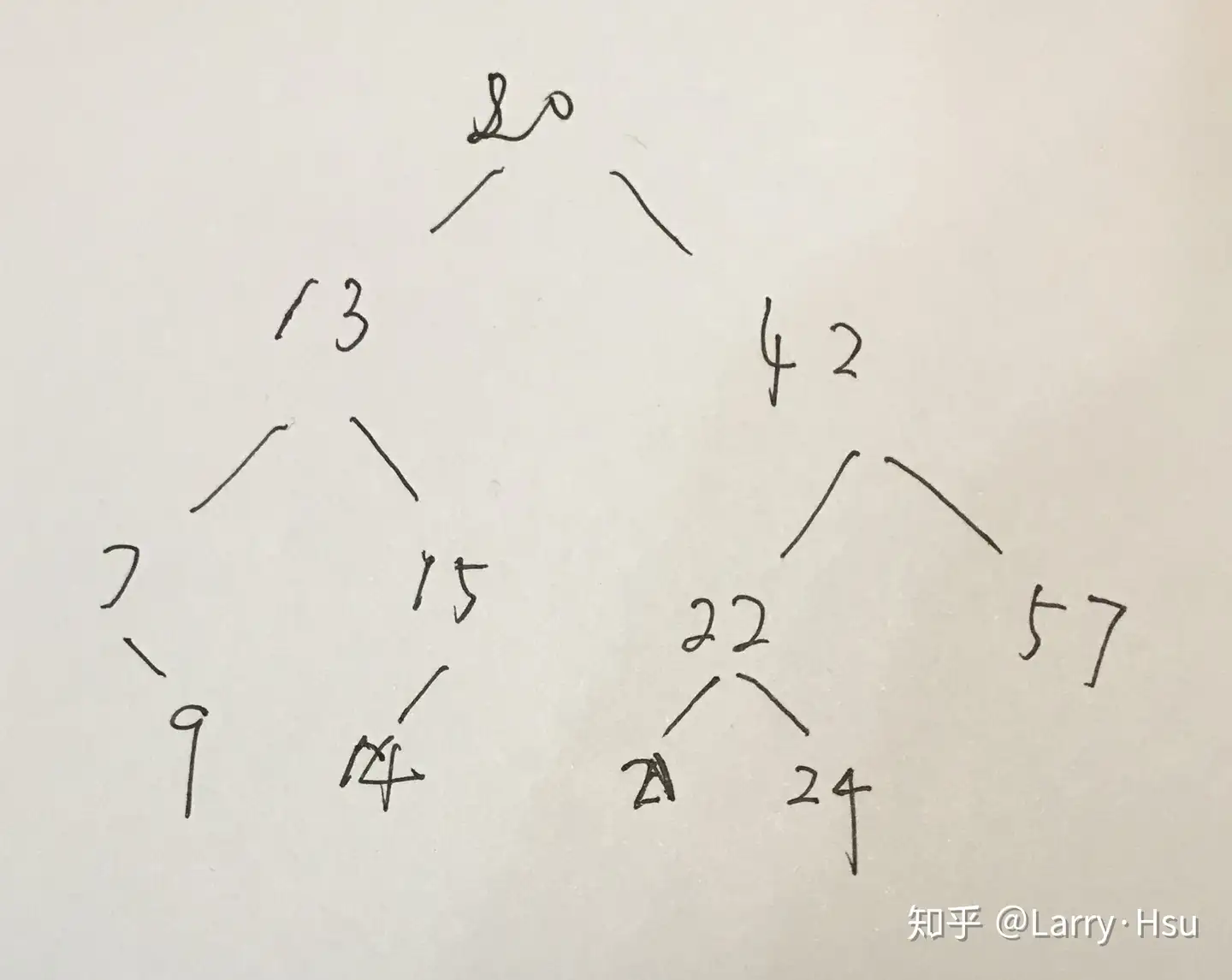
获取最大值试一下:
console.log(myTree.getMaxNode()); // Node {data: 57, left: null, right: null, count: 1}
可以看到值为57的节点确实没有左右子树。
最小值:
console.log(myTree.getMinNode()); // Node {data: 7, left: null, right: Node, count: 1}
可以看到值为7的节点只有右子树,与上图所示相同。
删除节点7,模拟下删除时有右子节点的情况:
myTree.remove(7);
console.log(myTree.getMinNode()); // Node {data: 9, left: null, right: null, count: 1}
可见值为9的节点取代了原来值为7的节点的位置。
删除节点42,模拟下删除时左右子树均存在的情况:
myTree.remove(42);
console.log(myTree.getMaxNode()); // Node {data: 57, left: Node, right: null, count: 1}
在删除值为42的节点时,使用的方法时寻找其右子树上的最大值,为57。将待删除的节点的值修改为57,然后在其右子树上删除值为57的节点即可。
根据返回的结果来看,删除后最大值为57,其右子树为空。可见是正确的。